| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- android
- chatGPT's answer
- 리눅스
- kotlin
- NIO
- 자바네트워크
- 인프라
- spring integration
- 시스템
- oracle
- 유닉스
- Database
- 코틀린
- 데이터베이스
- Java
- python
- spring data jpa
- jpa
- write by chatGPT
- 자바
- write by GPT-4
- 웹 크롤링
- 역학
- GPT-4's answer
- 고전역학
- flet
- JVM
- 파이썬
- 소프트웨어공학
- 자바암호
- Today
- Total
Akashic Records
이상 적분(Improper Integral) 본문

이상적분(Improper Integral)은 정적분의 개념을 확장한 것으로, 적분 구간이 무한대를 포함하거나 적분 함수가 특정 지점에서 무한대로 발산하는 경우에 정의됩니다. 이러한 적분은 수학에서 중요한 역할을 합니다. 이상적분은 크게 두 가지 유형으로 나뉩니다.
- 무한 구간에서의 적분: 적분 구간 중 적어도 하나가 무한대인 경우입니다. 예를 들어, $ \int_1^\infty \frac{1}{x^2} , dx $ 는 1부터 무한대까지의 구간에서 ( \frac{1}{x^2} )을 적분하는 것을 의미합니다. 이러한 적분은 구간을 한정된 값으로 대체한 후, 그 한계값을 계산함으로써 해결할 수 있습니다.
- 발산 지점에서의 적분: 적분 함수가 특정 지점에서 무한대로 발산하는 경우입니다. 예를 들어, $ \int_0^1 \frac{1}{\sqrt{x}} , dx $ 는 0에서 발산하지만, 적절한 방법을 사용하여 적분값을 구할 수 있습니다. 이 경우에도 적분 구간의 한계를 사용하여 접근합니다.
이상적분을 계산할 때는, 일반적으로 적분 구간을 나누거나 적분 변수에 대한 대체(limit substitution)를 통해 적분을 적절한 형태로 변환하고, 그 한계값을 구하는 방법을 사용합니다. 예를 들어, 무한 구간에서의 적분 $ \int_a^\infty f(x) , dx $ 는 $ \lim_{b \to \infty} \int_a^b f(x) , dx $ 로 표현되어 적분의 한계값을 구하는 과정을 포함합니다.
이러한 적분은 물리학과 공학에서 발생하는 다양한 문제, 특히 확률과 통계학에서 확률밀도함수를 통한 기대값 계산 등에서 중요하게 사용됩니다.
무한 구간에서의 이상적분
무한 구간에서의 이상적분을 이해하기 위해 다음 적분을 예로 들어 설명해 보겠습니다:
$ \int_1^\infty \frac{1}{x^2} , dx $
이 적분은 1부터 무한대까지의 구간에서 함수 $ \frac{1}{x^2} $ 를 적분하는 것을 의미합니다. 함수 $ \frac{1}{x^2} $ 는 $ x $ 가 커질수록 0에 수렴합니다. 이러한 이상적분을 계산할 때, 무한대로 확장되는 구간을 한계를 통해 접근하는 방법을 사용합니다.
계산 절차
- 한계의 정의:
적분의 무한 구간을 $ b $ 라는 유한한 값으로 대체하고, $ b $ 가 무한대로 갈 때의 한계를 계산합니다. 즉, 우리는 다음과 같은 한계를 계산하게 됩니다:
$ \lim_{b \to \infty} \int_1^b \frac{1}{x^2} , dx $ - 적분 계산:
적분 $ \int_1^b \frac{1}{x^2} , dx $ 을 계산합니다. 이 함수의 원시 함수는 ( -\frac{1}{x} )이므로, 적분은 다음과 같이 계산됩니다:
$ \int_1^b \frac{1}{x^2} , dx = \left[ -\frac{1}{x} \right]_1^b = -\frac{1}{b} + \frac{1}{1} $ - 한계값 계산:
이제 $ b $ 를 무한대로 보내면서 한계를 구합니다:
$ \lim_{b \to \infty} \left( -\frac{1}{b} + 1 \right) = \lim_{b \to \infty} -\frac{1}{b} + 1 = 0 + 1 = 1 $
따라서, $ \int_1^\infty \frac{1}{x^2} , dx = 1 $ 임을 알 수 있습니다. 이 결과는 해당 함수가 무한 구간에서 적분가능하며, 적분값이 유한함을 보여줍니다.
물리적 의미
이러한 종류의 이상적분은 물리학에서 중요합니다. 예를 들어, 중력장이나 전기장과 같은 퍼텐셜 에너지 계산에 사용될 수 있습니다. 무한 구간에서의 이상적분은 특정 범위에서의 물리적 현상을 전체 우주 또는 무한 공간으로 확장하여 해석하는 데 필요합니다. 이는 물리적 모델의 광범위한 적용성과 무한한 특성을 설명하는 데 중요한 도구입니다.
import numpy as np
import matplotlib.pyplot as plt
# Define the function and range
x = np.linspace(1, 20, 400)
y = 1 / x**2
# Create the plot
plt.figure(figsize=(10, 5))
plt.plot(x, y, label=r'$\frac{1}{x^2}$')
plt.fill_between(x, y, color='skyblue', alpha=0.4)
plt.title('Plot of $1/x^2$ from 1 to 20')
plt.xlabel('x')
plt.ylabel('y')
plt.ylim(0, 1)
plt.legend()
plt.grid(True)
plt.show()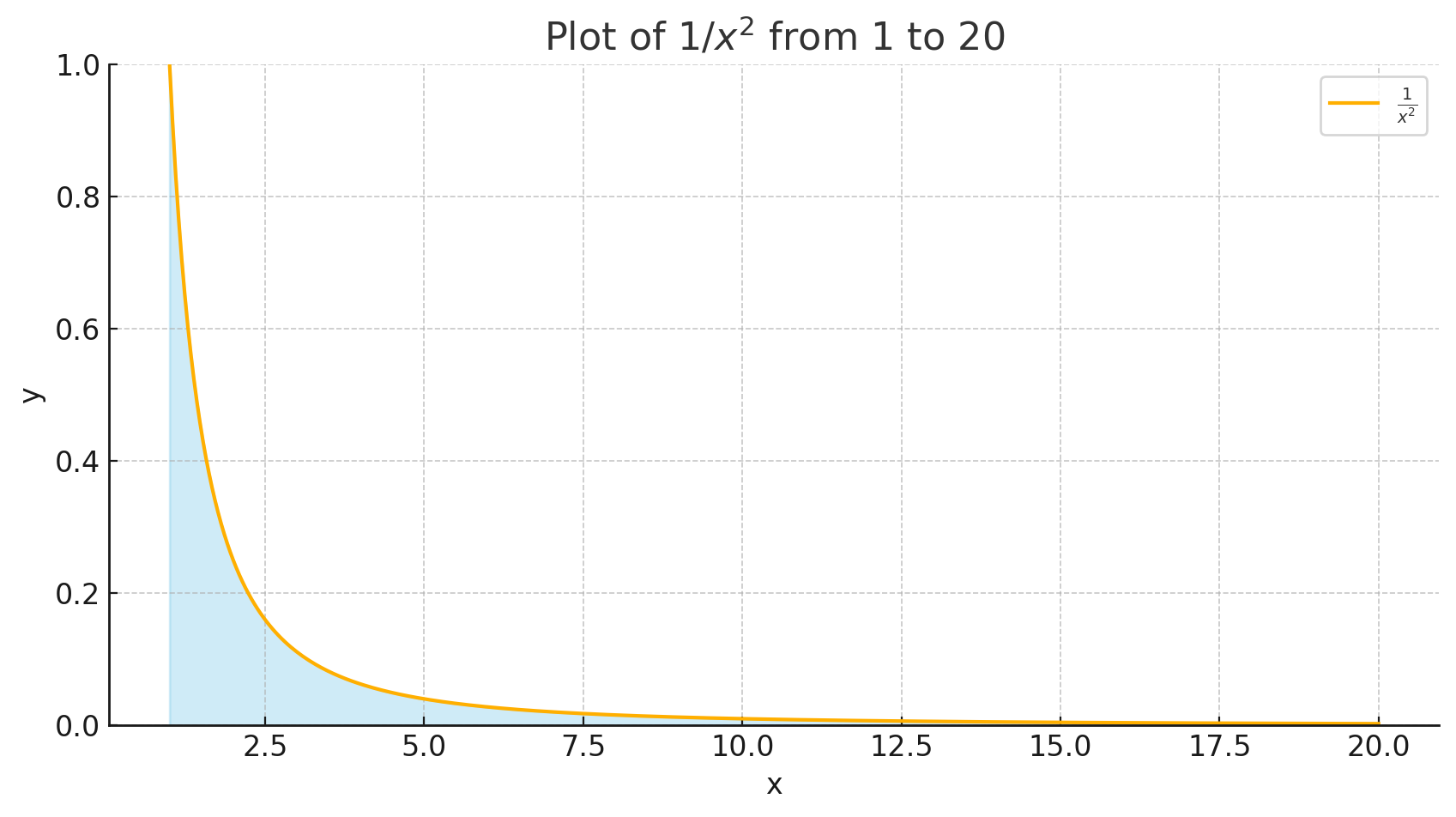
위 차트는 $ x $ 가 1에서 20까지 변화할 때 함수 $ \frac{1}{x^2} $ 의 그래프를 보여줍니다. 그래프에서 볼 수 있듯이, $ x $ 의 값이 증가함에 따라 함수의 값은 빠르게 0으로 수렴합니다. 이러한 특성은 이상적분 $ \int_1^\infty \frac{1}{x^2} , dx $ 의 값이 유한하다는 것을 시각적으로 잘 보여줍니다. 차트에 표시된 면적은 1부터 20까지의 적분값에 해당하는 영역을 나타내며, 이 값은 점점 1에 가까워지는 것을 알 수 있습니다.
발산 지점에서의 이상적분
발산 지점에서의 이상적분을 이해하기 위해 다음 적분을 예로 들어 설명하겠습니다:
$ \int_0^1 \frac{1}{\sqrt{x}} , dx $
이 적분은 0에서 1까지의 구간에서 함수 $ \frac{1}{\sqrt{x}} $ 를 적분하는 것을 의미합니다. 이 함수는 $ x = 0 $ 에서 발산합니다. 이러한 경우에는 적분 구간을 약간 조정하여 함수가 발산하지 않도록 하고, 적분의 한계값을 통해 접근합니다.
계산 절차
- 한계의 정의:
$ x = 0 $ 에서 발산하는 문제를 해결하기 위해 $ \epsilon $ 이라는 작은 양수를 도입하여 적분 구간을 $ [\epsilon, 1] $ 로 변경합니다. 그리고 $ \epsilon $ 을 0에 가깝게 보내면서 한계를 계산합니다:
$ \lim_{\epsilon \to 0^+} \int_\epsilon^1 \frac{1}{\sqrt{x}} , dx $ - 적분 계산:
주어진 적분 $ \int_\epsilon^1 \frac{1}{\sqrt{x}} , dx $ 은 $ \sqrt{x} $ 의 도함수가 $ \frac{1}{2\sqrt{x}} $ 임을 고려하면, 함수 $ \frac{1}{\sqrt{x}} $ 의 원시 함수는 $ 2\sqrt{x} $ 입니다. 따라서 적분은 다음과 같이 계산됩니다:
$ \int_\epsilon^1 \frac{1}{\sqrt{x}} , dx = \left[ 2\sqrt{x} \right]_\epsilon^1 = 2\sqrt{1} - 2\sqrt{\epsilon} = 2 - 2\sqrt{\epsilon} $ - 한계값 계산:
이제 $ \epsilon $ 을 0으로 보내면서 한계를 구합니다:
$ \lim_{\epsilon \to 0^+} (2 - 2\sqrt{\epsilon}) = 2 - 2 \times 0 = 2 $
따라서, $ \int_0^1 \frac{1}{\sqrt{x}} , dx = 2 $ 임을 알 수 있습니다. 이 결과는 해당 함수가 발산 지점에서도 적절한 한계를 사용하여 이상적분을 계산할 수 있음을 보여줍니다.
물리적 의미
발산 지점에서의 이상적분은 물리학, 특히 열역학과 유체역학에서 중요한 역할을 합니다. 이러한 적분은 무한대로 발산하는 특성을 모델링하고 이해하는 데 사용되며, 물리적 현상의 극한 상황을 설명하는 데 중요합니다. 이러한 적분들은 또한 특정 조건 하에서의 열적 또는 유체의 흐름 특성을 계산하는 데 사용될 수 있습니다.
# Define the function and range for the plot of 1/sqrt(x) from a small positive number close to 0 to 1
x = np.linspace(0.01, 1, 400)
y = 1 / np.sqrt(x)
# Create the plot
plt.figure(figsize=(10, 5))
plt.plot(x, y, label=r'$\frac{1}{\sqrt{x}}$')
plt.fill_between(x, y, color='skyblue', alpha=0.4)
plt.title('Plot of $1/\\sqrt{x}$ from 0.01 to 1')
plt.xlabel('x')
plt.ylabel('y')
plt.ylim(0, 10) # Set y-axis limit to better visualize the behavior near 0
plt.legend()
plt.grid(True)
plt.show()
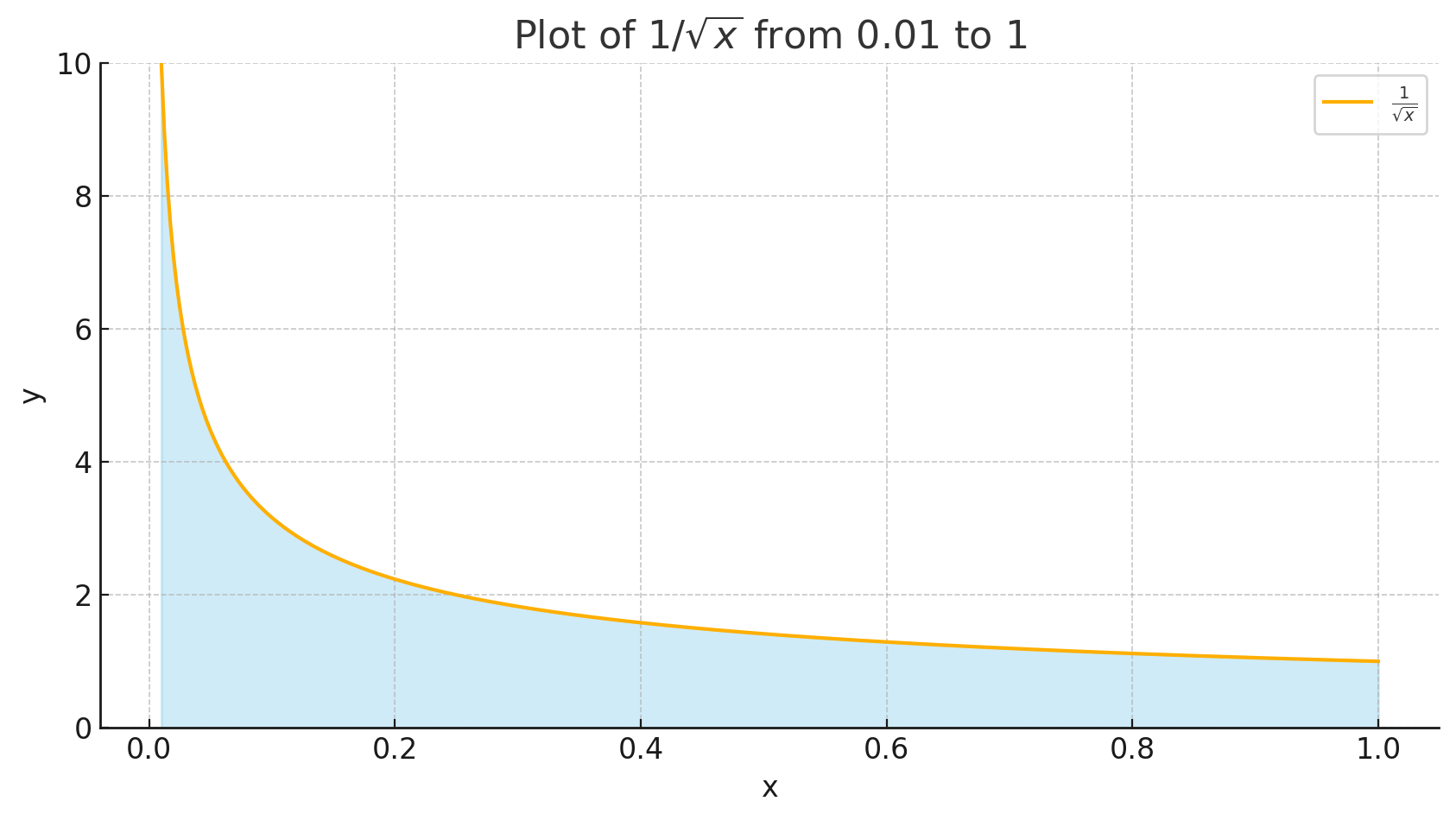
위 차트는 $ x $ 가 0.01부터 1까지 변화할 때 함수 $ \frac{1}{\sqrt{x}} $ 의 그래프를 보여줍니다. 차트에서 볼 수 있듯이, $ x $ 의 값이 0에 가까워질수록 함수의 값은 매우 빠르게 증가하며, 이는 함수가 $ x = 0 $ 에서 발산하는 것을 나타냅니다. 차트에 표시된 면적은 적분 $ \int_0^1 \frac{1}{\sqrt{x}} , dx $ 의 값이 2에 근접하는 것을 시각적으로 보여줍니다. 이러한 표현은 발산 지점에서의 이상적분을 계산할 때 어떻게 함수가 행동하는지 이해하는 데 도움을 줍니다.
'수학 Library' 카테고리의 다른 글
| 부분 적분(Integration by Parts) (0) | 2024.06.10 |
|---|---|
| 삼각치환 적분(Trigonometric Substitution) (1) | 2024.06.05 |
| 정적분의 치환적분 (0) | 2024.05.27 |
| 치환적분(substitution integration) 풀이 (0) | 2024.05.17 |
| 치환적분(substitution integration) 풀이 (0) | 2024.05.17 |





