728x90
정규분포 기반의 주가 판단 지표는 주가나 기술적 지표(예: 이동평균, 수익률 등)가 정규분포(Normal Distribution)를 따른다고 가정하고, 평균(μ)과 표준편차(σ)를 중심으로 주가가 어느 정도 '평균으로부터 벗어났는지'를 수치화하여 판단하는 방식입니다.
Z-Score (표준점수)
통계와 금융에서 모두 매우 유용하게 사용되는 개념으로, 어떤 값이 평균으로부터 얼마나 떨어져 있는지를 ‘표준편차’ 기준으로 나타낸 값입니다.
"데이터 값이 전체 평균에서 몇 개의 표준편차만큼 떨어져 있는가?"
$$ Z = \frac{X - \mu}{\sigma} $$
- X: 관측값 (예: 현재 주가)
- μ (뮤): 평균값 (예: 이동평균선)
- σ (시그마): 표준편차
직관적으로 이해하기
- Z = 0 → 평균과 동일
- Z = +1 → 평균보다 1표준편차 높음
- Z = -2 → 평균보다 2표준편차 낮음
주식 분석에서의 활용
주식 시장에서는 Z-Score를 통해 가격이 평균 대비 과하게 올랐거나 내렸는지를 판단합니다.
Z = (현재 주가 - 20일 이동평균) / 20일 표준편차
- Z > +2: 과매수 가능성 (되돌림 발생 가능)
- Z < -2: 과매도 가능성 (반등 발생 가능)
| Z-Score | 해석 | 가능성 |
| > +2 | 평균 대비 매우 높음 → 과매수 위험 | 매도 신호 가능 |
| 0 ~ +1 | 평균보다 약간 높음 | 정상 범위 |
| -1 ~ 0 | 평균보다 약간 낮음 | 정상 범위 |
| < -2 | 평균보다 매우 낮음 → 과매도 상태일 수 있음 | 매수 신호 가능 |
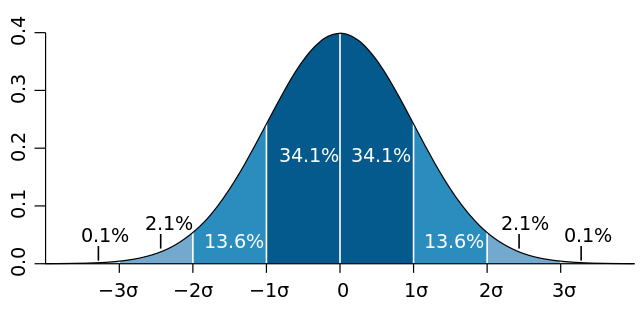
※ 정규분포를 가정하면 ±2σ 내에 약 95% 데이터가 분포합니다.
장점
- 단순하면서도 강력한 통계적 도구
- 다양한 지표(주가, 수익률, 거래량 등)에 적용 가능
- 시계열 데이터의 이상 탐지(Outlier Detection)로도 사용
단점 및 주의사항
- 정규분포 가정이 항상 성립하지 않음 (주가는 fat-tail 현상 있음)
- 급변하는 시장에선 평균과 표준편차가 빠르게 바뀔 수 있음
- Z-Score만으로 매수/매도 결정을 내리는 건 위험 → 다른 지표와 병행 필요


Fat-tail 현상(fat-tail phenomenon)
통계학과 금융에서 매우 중요한 개념으로, 특히 주식이나 환율처럼 극단적인 변화가 발생할 수 있는 데이터를 이해하는 데 핵심적인 역할을 합니다. Fat-tail은 말 그대로 “꼬리가 두껍다”는 뜻입니다.
정규분포(종 모양 곡선)는 양 끝이 빠르게 수렴하지만, Fat-tail 분포는 극단값이 나올 확률이 상대적으로 높습니다.
정규분포
- ±2σ를 벗어날 확률이 약 5%밖에 안 됨
Fat-tail 분포
꼬리 부분이 천천히 줄어들며, 극단적인 사건이 더 자주 발생

"정규분포는 세상이 예측 가능한 곳이라고 가정하지만, fat-tail은 현실의 충격적인 사건(폭락, 전쟁, 금융위기 등)이 실제로 꽤 자주 일어남을 반영한다"는 뜻입니다.
금융시장과 Fat-tail
- 주가 폭락, 환율 급변, 유가 쇼크처럼 예외적 사건이 정규분포로는 설명되지 않음
- 정규분포에 따르면 하루에 -10% 급락할 확률은 거의 0%인데, 현실에서는 자주 발생
대표적 예:
- 2008 금융위기
- 2020 코로나19 폭락
- 루나/UST 폭락
정규분포 vs Fat-tail 비교
| 항목 | 정규분포 (Normal) | Fat-tail 분포 |
| 중심 밀집 | 매우 강함 | 중간보다 극단치도 자주 발생 |
| 극단값 발생 확률 | 매우 낮음 (거의 없음) | 꽤 있음 (현실적으로 의미 있음) |
| 위험 모델링 | 낙관적 (위험 과소평가) | 비관적 (위험 현실적으로 반영) |
728x90
'All at Once' 카테고리의 다른 글
| 정규분포 기반 주가 판단 지표 - Percent B, Probability of Mean Reversion (0) | 2025.05.21 |
|---|---|
| 정규분포 기반 주가 판단 지표 - Bollinger Bands (볼린저 밴드) (0) | 2025.05.15 |
| 인플레이션과 중앙은행(FED)의 경제 안정 전략 (1) | 2024.07.09 |
| 여러가지 경제지표 (0) | 2024.07.09 |
| 경제 지표(GDP, GDI)와 경기 침체 (0) | 2024.07.08 |