
단진동(Simple Harmonic Motion, SHM)은 시간에 따라 변화하는 양이 정현파(sine wave) 형태로 변화하는 가장 기본적인 진동 운동입니다. 이 운동은 복원력이 작용하는 시스템에서 발생하며, 이 복원력은 변위에 비례하고 변위의 방향과 반대 방향으로 작용합니다. 단진동은 물리학에서 광범위하게 연구되며, 많은 자연 현상과 기술적 응용 분야에서 중요한 역할을 합니다.
단진동의 특성
- 복원력: 단진동을 하는 시스템에는 위치의 변화에 비례하여 작용하는 복원력이 있습니다. 예를 들어, 이상적인 진자나 질량이 달린 스프링 시스템에서 볼 수 있습니다.
- 정현파 운동: 단진동의 시간에 따른 변위는 코사인(cos)이나 사인(sin) 함수로 표현될 수 있으며, 이는 정현파 형태를 나타냅니다.
- 주기와 진폭: 단진동은 주기적인 운동으로, 진폭(최대 변위)과 주기(한 사이클을 완료하는 데 걸리는 시간)를 가집니다.
- 에너지 보존: 이상적인 단진동 시스템에서는 운동 에너지와 위치 에너지가 지속적으로 변환되지만, 시스템의 총 에너지는 보존됩니다.
단진동의 예
- 스프링-질량 시스템: 스프링에 연결된 질량이 평형 위치에서 변위될 때 발생합니다. 복원력은 스프링 상수와 변위의 곱으로 나타납니다.
- 단진자: 작은 진폭으로 진동하는 단진자는 단진동의 예입니다. 여기서 복원력은 중력에 의해 생성됩니다.
수학적 표현(변위)
단진동에서 변위 (x)는 시간 (t)에 대한 함수로 다음과 같이 표현될 수 있습니다:
x(t) = A cos(ωt + ϕ)
여기서,
- A는 진폭(최대 변위),
- ω 는 각주파수(한 사이클을 완료하는 데 걸리는 각도),
- ϕ 는 위상 상수(시작점에서의 변위),
- t 는 시간입니다.
각주파수 ω 는 주기 (T) 또는 진동수 (f)와 관련이 있으며,

로 표현됩니다.
단진동은 물리학뿐만 아니라 엔지니어링, 천문학, 음향학 등 다양한 분야에서도 중요한 개념입니다.
속도
단진동하는 물체의 속도는 변위를 시간에 대해 미분함으로써 구할 수 있습니다. 따라서, 속도 v(t)는 다음과 같이 표현됩니다:

1. 미분의 체인 규칙(chain rule)에 따라 𝜔𝑡+𝜙를 먼저 t에 대해 미분합니다.
2. 코사인 함수의 미분은 마이너스 사인 함수입니다.
속도는 변위의 최대값을 갖는 위치에서 0이 되며, 평형 위치를 통과할 때 최대가 됩니다.
가속도
마찬가지로, 가속도는 속도를 시간에 대해 미분함으로써 구할 수 있습니다. 가속도 a(t)는 다음과 같이 표현됩니다:

속도 𝑣(𝑡)는 시간에 따른 위치의 변화율로, 위의 미분을 통해 계산됩니다. 이 속도 함수를 다시 𝑡에 대해 미분하면 가속도 𝑎(𝑡)를 얻게 됩니다:
이는 가속도가 변위에 비례하며, 변위의 방향과 반대임을 나타냅니다. 이는 SHM의 정의와 일치합니다: 복원력(가속도에 비례하는 힘)은 변위에 비례하며 변위와는 반대 방향으로 작용합니다.
요약
- 속도와 가속도는 모두 시간에 따라 정현파 형태로 변화합니다.
- 속도는 변위의 시간에 대한 첫 번째 미분이며, 가속도는 변위의 시간에 대한 두 번째 미분입니다.
- 속도는 평형 위치에서 최대가 되며, 변위가 최대일 때 0이 됩니다.
- 가속도는 변위에 직접 비례하며 변위의 방향과 반대입니다. 이는 복원력의 특성을 반영합니다.
이 공식에서 확인할 수 있는 몇 가지 주요 사실은 다음과 같습니다:
- 복원력과의 관계: 가속도는 복원력에 직접적으로 비례하고, 복원력은 변위에 비례합니다. 이는 Hooke의 법칙을 연상시키며, 이상적인 스프링에서 발견되는 행동을 설명합니다. 스프링의 경우 복원력은 스프링 상수 ( k )와 변위 ( x )의 곱으로 나타낼 수 있으며, 이것이 바로 가속도에 영향을 줍니다.
- 위치에너지와의 관계: 가속도가 변위에 정비례하면, 단진동 시스템 내의 총 에너지는 운동 에너지와 위치 에너지 사이에서 변환되지만 보존됩니다. 즉, 변위가 최대일 때 위치 에너지가 최대가 되고 운동 에너지가 최소가 됩니다. 반대로, 변위가 최소(즉, 평형점)일 때 운동 에너지가 최대가 됩니다.
- 주기와 진폭: 변위와 가속도의 관계를 통해, 단진동 시스템의 주기 ( T )와 진폭 ( A )가 해당 시스템의 고유한 특성임을 알 수 있습니다. 이러한 값들은 외부에서 가해진 힘의 크기에 의존하지 않습니다.
- 감쇠와 공명: 실제 세계의 단진동 운동은 감쇠력(예: 마찰, 공기 저항)의 영향을 받을 수 있으며, 이러한 감쇠력은 변위와 가속도 사이의 관계를 변화시킬 수 있습니다. 감쇠가 없는 이상적인 시스템에서는 단진동이 무한히 지속될 수 있지만, 감쇠가 있는 시스템에서는 운동이 점차 줄어들게 됩니다. 또한, 외부에서 가해지는 주기적인 힘이 시스템의 자연 주기와 일치할 때 공명이 발생할 수 있으며, 이 경우 진폭이 크게 증가할 수 있습니다.

수평 용수철 진자는 용수철의 한쪽 끝이 고정되어 있고 다른 쪽 끝에 질량 ( m )이 부착되어 있으며 수평면 위에서 진동하는 시스템을 말합니다. 이 시스템에서 질량은 용수철의 복원력에 의해 좌우로 진동하게 됩니다. 수평 용수철 진자의 운동은 간단한 단진동(simple harmonic motion, SHM)의 한 예로서, 용수철 상수 ( k )와 질량 ( m )에 의해 그 특성이 결정됩니다.
용수철 진자의 운동 방정식
수평 용수철 진자의 운동은 Hooke의 법칙에 따라 복원력이 변위에 비례하고, 변위의 방향과 반대 방향으로 작용한다는 것을 기반으로 합니다. 변위를 ( x )라고 할 때, 복원력 ( F )는 다음과 같이 표현됩니다:
F=−kx
여기서 k 는 용수철의 상수입니다. 이 복원력은 뉴턴의 두 번째 운동 법칙에 의해 가속도 ( a )를 유발합니다:
F=ma
따라서, 가속도는 다음과 같이 표현됩니다:

이는 단진동 운동의 기본 형태와 같습니다. 위 식은 가속도가 변위에 비례하고 반대 방향임을 보여주며, 이는 SHM의 정의와 일치합니다.
진동 주기와 주파수
수평 용수철 진자의 주기 T와 주파수 f는 용수철 상수 k와 질량 m에 의해 결정됩니다:

에너지
수평 용수철 진자에서는 운동 에너지와 탄성 위치 에너지가 지속적으로 서로 변환됩니다. 이때 시스템의 총 에너지는 보존됩니다. 탄성 위치 에너지 U는 다음과 같이 표현됩니다:
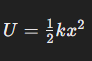
그리고 운동 에너지 K는 다음과 같이 표현됩니다:
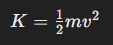
수평 용수철 진자는 실험실 환경에서 고전역학을 연구하는 데 자주 사용되는 시스템으로, 에너지 보존, 감쇠 운동, 강제 진동 등 다양한 물리 현상을 모델링하는 데 유용합니다.
'과학 Library' 카테고리의 다른 글
| 제1 우주 속도, 제2 우주 속도 (0) | 2024.04.12 |
|---|---|
| 뉴턴의 중력 이론 (만유인력) (0) | 2024.04.12 |
| 일정한 속력으로 움직이는 원운동의 속력과 각속도의 관계 (0) | 2024.04.09 |
| 충돌 전후의 상대 속도로 반발계수 구하기 (0) | 2024.04.04 |
| 두 물체의 충돌과 운동량 (0) | 2024.04.03 |



