충격량(Impulse)과 운동량

Here's an illustration designed to visualize the concept of impulse in classical mechanics. It shows a soccer ball being kicked, illustrating how the force applied over a time interval results in a change in the ball's momentum. The annotations highlight the applied force, the time interval during which the force is applied, and the resulting change in momentum, aiming to help understand how impulse leads to momentum change, emphasizing the principles of momentum conservation.

 

고전역학에서 충격량(Impulse)은 힘(force)이 시간(time) 동안 작용할 때 물체의 운동량(momentum) 변화를 나타냅니다. 운동량은 물체의 속도와 질량의 곱으로, 물체의 운동 상태를 나타내는 물리량입니다. 충격량은 다음과 같은 공식으로 표현됩니다:

충격량 정의

여기서,

• J는 충격량,
• F는 힘,
• Δt는 힘이 작용한 시간의 변화량입니다.

충격량의 단위는 뉴턴초(Ns)입니다. 이는 힘(뉴턴)이 시간(초) 동안 작용한 양을 나타냅니다.

또한, 충격량은 물체의 운동량의 변화와 직접적으로 관련되어 있으며, 다음과 같은 관계가 있습니다:

J = Δp

 

여기서 Δp는 운동량의 변화량입니다. 이는 물체의 초기 운동량과 최종 운동량의 차이로, 충격량은 물체에 작용한 힘의 총합이 시간에 따라 얼마나 변화시켰는지를 나타냅니다. 예를 들어, 축구공을 차는 행위에서 발이 공에 닿는 순간 발이 공에 가하는 힘과 그 힘이 작용하는 시간을 곱한 것이 공의 운동량 변화, 즉 충격량이 됩니다. 이 원리는 충돌과 같은 다양한 물리적 상황에서 중요하게 적용됩니다.

충격량과 운동량의 관계

충격량과 운동량의 관계는 고전역학의 핵심 원리 중 하나입니다. 이 관계는 뉴턴의 제2법칙을 바탕으로 하며, 충격량이 물체의 운동량 변화와 직접적으로 연결되어 있다는 것을 설명합니다.

운동량 (Momentum)

운동량은 물체의 운동 상태를 나타내는 물리량으로, 물체의 질량과 속도의 곱으로 정의됩니다. 운동량의 식은 다음과 같습니다:

p = mv

 

여기서 p는 운동량, m은 물체의 질량, v는 물체의 속도입니다.

충격량 (Impulse)

충격량은 힘과 힘이 작용하는 시간의 곱으로, 물체에 가해진 힘의 "충격"을 측정하는 데 사용됩니다. 충격량의 식은 다음과 같습니다:

J = F Δ t

 

여기서J는 충격량, F는 힘, Δt는 힘이 작용하는 시간입니다.

 

충격량은 물체의 운동량의 변화와 직접적으로 관련이 있습니다. 즉, 물체에 가해진 충격량은 물체의 초기 운동량과 최종 운동량의 차이, 즉 운동량의 변화와 같습니다. 이 관계는 다음과 같이 수식으로 나타낼 수 있습니다:

 

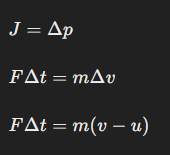
여기서 m은 물체의 질량, u는 초기 속도, v는 최종 속도, F는 가해진 힘, Δt는 힘이 작용한 시간, J는 충격량, Δp는 운동량의 변화입니다.

 

이 관계는 물체에 힘이 작용할 때 물체의 운동 상태가 어떻게 변하는지를 설명해 줍니다. 예를 들어, 축구공에 발을 강하게 차면(큰 충격량을 주면), 공의 운동량은 크게 변하게 됩니다. 이 원리는 충돌, 발사체 운동, 스포츠 과학 등 다양한 분야에서 중요한 역할을 합니다.