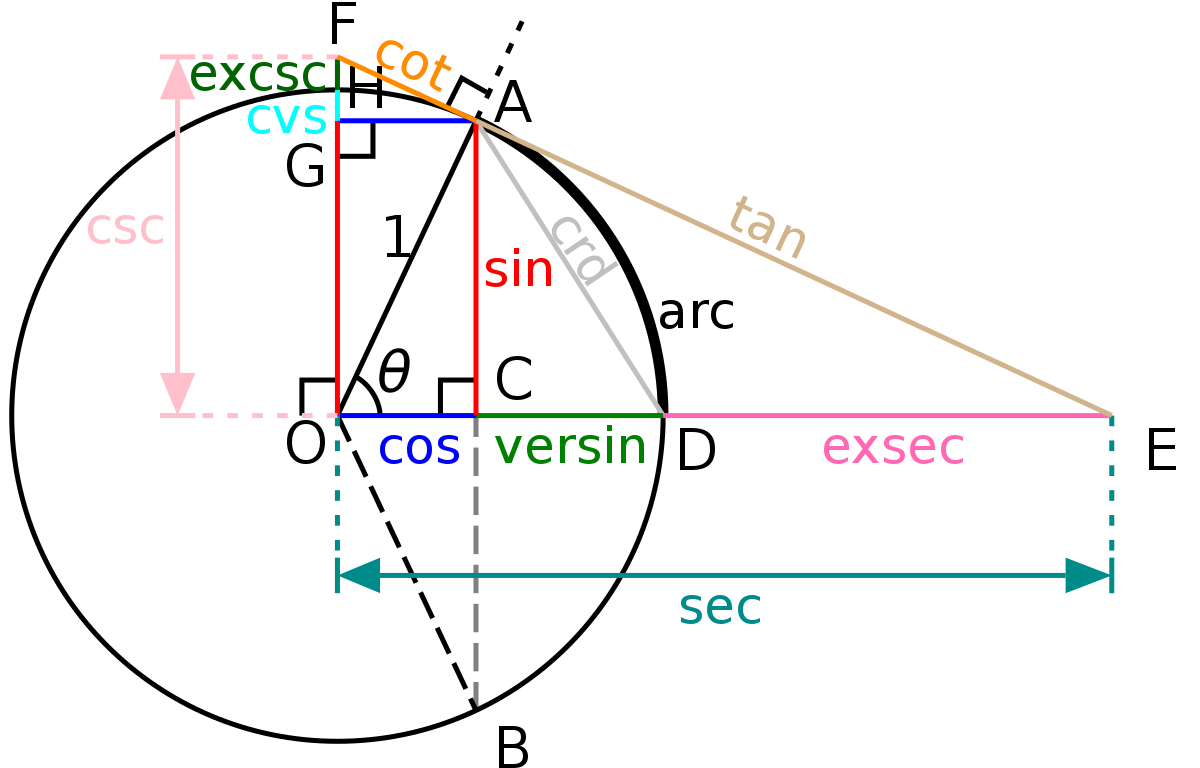
삼각함수는 삼각형의 세 변의 비율을 나타내는 수학적 함수입니다. 가장 흔히 알려진 삼각함수에는 사인(sin), 코사인(cos), 탄젠트(tan) 등이 있습니다.
- 사인(sin): 주어진 각도의 대해 세워진 직각 삼각형에서, 빗변에 대한 반대변의 비율을 의미합니다.
- 코사인(cos): 주어진 각도의 대해 세워진 직각 삼각형에서, 빗변에 대한 인접변의 비율을 의미합니다.
- 탄젠트(tan): 주어진 각도의 대해 세워진 직각 삼각형에서, 반대변에 대한 인접변의 비율을 의미합니다. 탄젠트는 또한 사인과 코사인의 비율(sin/cos)로도 정의됩니다.
이 외에도 코시컨트(csc), 시컨트(sec), 코탄젠트(cot) 등의 역삼각함수도 있습니다.
삼각함수는 원의 단위로 각도를 측정하는 데에도 사용되며, 이를 라디안(radian)이라고 부릅니다. 원주율 π는 원의 지름에 비해 원주의 길이를 나타내는 수로, 180도를 라디안으로 변환하면 π가 됩니다.
삼각함수는 물리, 공학, 컴퓨터 과학 등 여러 학문에서 널리 활용되는 중요한 개념입니다.
삼각함수는 여러 학문과 산업 분야에서 중요한 역할을 합니다. 그 사용 사례는 아래와 같습니다:
- 물리학: 물리학에서 삼각함수는 주로 각도, 회전, 진동, 파동 등을 설명하는데 사용됩니다. 예를 들어, 간단한 조화 진동자는 사인과 코사인 함수로 표현되며, 이는 물리학에서 많은 현상을 모델링하는데 중요합니다.
- 공학: 공학에서 삼각함수는 다양한 현상을 분석하고 설계하는 데 필요합니다. 예를 들어, 전기 공학에서는 전기 신호(주로 사인과 코사인 파)를 분석하고 조작하는 데 삼각함수를 사용합니다. 또한, 구조 공학에서는 건물이나 다리 등의 안정성을 평가하거나 설계하는 데 삼각함수를 사용할 수 있습니다.
- 컴퓨터 과학: 컴퓨터 그래픽에서, 삼각함수는 회전, 스케일링, 편향 등의 변환을 수행하는데 사용됩니다. 또한, 알고리즘 설계에도 삼각함수가 사용될 수 있습니다.
- 음악과 음향학: 사운드 분석 및 생성에 있어서 삼각함수는 중요한 역할을 합니다. 파형을 생성하거나 음향 신호를 분석하는데 삼각함수를 사용합니다.
- 지리학과 천문학: 지구의 곡률을 고려한 거리 측정, 천체의 움직임 모델링 등에 삼각함수가 사용됩니다.
- 경제학: 경제학에서 주기적인 변동을 보이는 현상(계절성 등)을 분석하거나 예측하는 데 삼각함수를 활용할 수 있습니다.
이 외에도 삼각함수는 생물학, 화학, 통계 등 많은 학문에서도 사용되며, 실제 생활에서도 다양한 현상을 이해하는 데 도움을 줍니다.
삼각함수에는 다양한 중요한 법칙들이 있습니다. 아래는 그 중 일부입니다:
- 덧셈 및 뺄셈 공식:
- sin(a + b) = sin(a)cos(b) + cos(a)sin(b)
- cos(a + b) = cos(a)cos(b) - sin(a)sin(b)
- sin(a - b) = sin(a)cos(b) - cos(a)sin(b)
- cos(a - b) = cos(a)cos(b) + sin(a)sin(b)
- tan(a + b) = (tan(a) + tan(b)) / (1 - tan(a)tan(b))
- tan(a - b) = (tan(a) - tan(b)) / (1 + tan(a)tan(b))
- 이중각 공식:
- sin(2a) = 2sin(a)cos(a)
- cos(2a) = cos²(a) - sin²(a) = 2cos²(a) - 1 = 1 - 2sin²(a)
- tan(2a) = 2tan(a) / (1 - tan²(a))
- 반각 공식:
- sin²(a) = 1/2 * (1 - cos(2a))
- cos²(a) = 1/2 * (1 + cos(2a))
- tan(a/2) = ±sqrt{(1 - cos(a)) / (1 + cos(a))} = (1 - cos(a)) / sin(a) = sin(a) / (1 + cos(a))
- 피타고라스의 삼각함수 버전:
- sin²(a) + cos²(a) = 1
- 1 + tan²(a) = sec²(a)
- 1 + cot²(a) = csc²(a)
- 주기성 및 대칭성:
- sin(a + 2π) = sin(a)
- cos(a + 2π) = cos(a)
- tan(a + π) = tan(a)
- sin(-a) = -sin(a)
- cos(-a) = cos(a)
- tan(-a) = -tan(a)
이 법칙들은 삼각함수를 이해하고 사용하는 데 필수적이며, 다양한 수학적 문제를 해결하는 데 유용합니다.
아래는 일부 각도에 대한 사인, 코사인, 탄젠트의 값들을 나타낸 표입니다. 라디안 값과 각도 값 모두를 표시해 두었습니다.
| 각도 (도) | 각도 (라디안) | sin(θ) | cos(θ) | tan(θ) |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 |
| 30 | π/6 | 1/2 | √3/2 ≈ 0.866 | 1/√3 ≈ 0.577 |
| 45 | π/4 | √2/2 ≈ 0.707 | √2/2 ≈ 0.707 | 1 |
| 60 | π/3 | √3/2 ≈ 0.866 | 1/2 | √3 ≈ 1.732 |
| 90 | π/2 | 1 | 0 | 정의되지 않음 |
| 120 | 2π/3 | √3/2 ≈ 0.866 | -1/2 | -√3 |
| 135 | 3π/4 | √2/2 ≈ 0.707 | -√2/2 ≈ -0.707 | -1 |
| 150 | 5π/6 | 1/2 | -√3/2 ≈ -0.866 | -1/√3 ≈ -0.577 |
| 180 | π | 0 | -1 | 0 |
| 210 | 7π/6 | -1/2 | -√3/2 ≈ -0.866 | 1/√3 ≈ 0.577 |
| 225 | 5π/4 | -√2/2 ≈ -0.707 | -√2/2 ≈ -0.707 | 1 |
| 240 | 4π/3 | -√3/2 ≈ -0.866 | -1/2 | √3 |
| 270 | 3π/2 | -1 | 0 | 정의되지 않음 |
| 300 | 5π/3 | -√3/2 ≈ -0.866 | 1/2 | -√3 |
| 315 | 7π/4 | -√2/2 ≈ -0.707 | √2/2 ≈ 0.707 | -1 |
| 330 | 11π/6 | -1/2 | √3/2 ≈ 0.866 | -1/√3 ≈ -0.577 |
| 360 | 2π | 0 | 1 | 0 |
이 표를 참고로 삼각함수의 값들을 이해하고 활용할 수 있습니다.
사인 법칙은 삼각형의 세 변과 세 각도 간의 관계를 설명하는 중요한 공식입니다. 어떤 삼각형 ABC에서, 각 A, B, C가 각각 삼각형의 변 a, b, c에 대응한다면, 사인 법칙은 다음과 같이 표현됩니다:
a/sin(A) = b/sin(B) = c/sin(C)
이 식은 삼각형의 모든 변과 각이 비례 관계에 있다는 것을 나타냅니다. 이 사인 법칙은 임의의 삼각형 (직각 삼각형뿐만 아니라)에 대해 성립하며, 삼각형의 세 변 중 두 개와 한 각이 주어졌을 때, 다른 각이나 변을 찾는 데 사용됩니다.
코사인 법칙은 삼각형의 세 변의 길이와 하나의 각도 사이의 관계를 나타내는 중요한 공식입니다. 직각 삼각형뿐만 아니라 모든 종류의 삼각형에 적용할 수 있습니다.
코사인 법칙은 다음과 같이 표현됩니다:
a² = b² + c² - 2bc cos(A)
여기서 a, b, c는 삼각형의 변의 길이이고, A는 변 a에 대한 각도입니다.
코사인 법칙은 세 변의 길이가 모두 주어졌을 때 하나의 각도를 찾거나, 두 변의 길이와 이들 사이의 각도가 주어졌을 때 세 번째 변의 길이를 찾는 데 유용합니다.
같은 방식으로, 다른 변에 대한 코사인 법칙도 표현할 수 있습니다:
b² = a² + c² - 2ac cos(B)
c² = a² + b² - 2ab cos(C)
이렇게, 각 각도에 대응하는 변의 길이를 구하는 공식이 세 개 있습니다.
'수학 Library' 카테고리의 다른 글
| 라플라스 변환(Laplace Transform) (0) | 2023.05.26 |
|---|---|
| 자연상수 e (0) | 2023.05.22 |
| 페르마의 마지막 정리 (0) | 2023.04.05 |
| 미분 가능성 연속성 (0) | 2023.03.24 |
| 평균변화율과 미분계수 (0) | 2023.03.17 |


